LevelDB Data Structures Serials I: Skip List
I’ve heard a lot about LevelDB, now I had a chance to skim through the code on a whim, and it deserves its reputation. If you’re interested in Storage Engine, if you want to use C++ gracefully, or if you want to learn how to organize codes, I recommend it strongly. Let alone the authors are Sanjay Ghemawat and Jeff Dean.
If I don’t take some notes after reading it, I’m sure I’ll quickly forget about it, given my poor memory. So I wanted to write something about the beauty of LevelDB, but I didn’t want to follow the usual way of starting with an architectural overview and ending with a module analysis. During the days of reading the code, I was trying to figure out how to start. When I was about to finish reading the code, what struck me most was the subtlety of LevelDB’s data structures: fitting the context, building from scratch, tailoring well, and coding excellent. Then, let’s start the LevelDB series with these little corner pieces.
In this series, I would like to share three classic data structures that are widely used, namely Skip List for fast reading and writing in memory, Bloom Filter for accelerating SSTable lookup and LRUCache for caching SSTable blocks. This is the first article, Skip List.
Requirements
LevelDB is an embedded KV storage engine, which in essence provides only three interfaces: Put(key, val), Get(key)->val, Delete(key)operations on data items (key, val). In terms of implementation, LevelDB doesn’t delete the data immediately when it receives a delete request but instead writes a special tag for the key indicating the key doesn’t exist when it is accessed, thus converting Delete to Put and thus reducing the three interfaces to two. After this cutting, all that remains is the performance trade-off between Put and Get, and LevelDB’s choice is: Tradeoff some Get performance for strong Put performance, and then go back to optimize the Get.
We know that in the memory hierarchy, memory access is much faster than that on disk, so LevelDB was designed as:
Writes (Put): Let all writes fall into memory and then flush them to disk in batch once they reach a threshold.
Reads (Get): As data accumulates by being written over time, only a small size of data is in memory and most of them reside on disk. When a read request comes in and is not hit in memory, you need to search it on disk.
To improve write performance while optimizing read performance, the in-memory storage structure needs to support both efficient inserts(for write) and lookups(for read).
When I know about LevelDB for first, I naturally thought that the in-memory structure (MemTable) was implemented as a BST(balanced search tree), such as a red-black tree, AVL tree, etc., in which case, it could guarantee that the time complexity of both insertion and lookup is log (n), but after reading the source code and realized that it is a Skip List. The advantage of Skip List over a balanced tree is that they simplify the implementation greatly while maintaining a good lookup and insert performance at the same time.
Besides, the data structure needs to support efficient range scans to flush data to disk periodically. In summary, the in-memory data structure (MemTable) of LevelDB requires:
Efficient lookup
Efficient insertion
Efficient range scan
Theory
Paper Skip Lists: A Probabilistic Alternative to Balanced Trees was proposed by William Pugh in 1990. As can be seen from the title, the author aimed to design a data structure that could replace balanced trees, as he mentioned in the beginning:
Skip lists are a data structure that can be used in place of balanced trees.
Skip lists use probabilistic balancing rather than strictly enforced balancing and as a result the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.
There is a key word in this passage: Probabilistic Balancing, which will be left untouched for now. In the following part, we will measure SkipList from two perspectives: linked list vs skip list, and skip list vs balanced trees. And then come back for the key word.
From LinkedList to SkipList
Essentially, a SkipList is a LinkedList with some extra pointers. To understand what it means, let’s consider the way of optimizing the lookup performance of an ordered linked list.
Suppose we have an ordered linked list, which is known to have an O(n)complexity of lookup and insertion. We cannot perform binary lookups on the linked list but on arrays, because we cannot access data in the linked list for O(1) complexity , thus cannot cut off half size of candidates quickly for every seek. So how can we improve a linked list to make it support binary search?
One simple way is to construct a map from subscripts to nodes. This would allow binary search, but each insertion would cause a whole adjustment of the map, which has an O(n) complexity.
Another way is to add pointers so that you can access any other node in each node directly. That would require constructing a fully connected map, which would take up too much space. Besides, each node insertion will still cause O(n) pointers added.
SkipList leverages an ingenious way to solve this: skip sampling to build indexes and reduce the sampling frequency bottom-up. I will explain it in more detail below using a figure from the paper.

As shown above, we initially have an ordered linked list in Fig a with a dummy head node, which has an O(N) complexity for lookup. Then, we perform a skip-step sampling and connected the sampled nodes and then we get the Fig b, which has a O(N/2+1) complexity for lookup. Later, we sample again based on the nodes sampled last time and connect the nodes with pointers to get Fig c. The lookup complexity then becomes O(N/4+2). Thereafter, we repeat this sampling and connect again and again, until there is only one node left, as shown in Fig e. The lookup complexity at this point can be seen to be O(logN).
We achieve this lookup performance at the cost of a bunch of pointers added. One question raised, how many pointers are there? Let’s consider this problem step by step. As can be seen from the figure, will add the same pointers with sampled nodes each time. And our sampling strategy is based on the previous set each time, with N nodes initially, and one node remaining finally. Sum them, we will get (N/2 + N/4 + … + 1) = N. That is to say, we add the same pointers with the nodes in the linked list to get a skip list.
There is a hidden question here: what is the insertion time complexity of this structure? For now, we touch on the nature of the problem gradually: how should we perform the insertion?
From BalancedTrees to SkipList
In practice, we implement the dictionary or ordered array as BST(binary search trees). During insertion, if the data comes with good randomness in the key space, then the BST can gain good query performance. On the other hand, if the data comes sequentially, the search tree will become severely unbalanced, in which case, both lookup and insertion performance will degrade significantly.
To maintain the performance, we need to adjust the imbalance when we find it, hence we have the AVL tree or the red-black tree. As you can see, the rotation strategy of AVL and the color labeling strategy of red-black trees are both too complex to remember. Hence, it is impossible to write them from scratch in an interview.
The SkipList, on the other hand, uses a very clever transformation that greatly simplifies the implementation of insertion, while guaranteeing the same lookup performance. We cannot make sure that all insertions have good randomness, or balance, in key space; but we can control the balance of some other dimensions. For example, the probabilistic balance of the distribution of the number of pointers to each node in the SkipList.
Probabilistic Balance
To make it clearer, let’s go through the structure of a SkipList and the concepts involved. Each node in a SkipList has [1, MaxLevel] pointers and a node with k pointers is called a level k node; the maximum level of all nodes is the maximum level(MaxLevel) in the SkipList. Besides, A SkipList has a dummy header node with MaxLevel pointers.
It becomes a problem to insert a node if we use the procedure introduced in understanding SkipList. For one thing, how many pointers does the inserted node need to have? How can we ensure that the lookup performance does not degrade after the insertion (i.e. maintain a balanced sampling)?
To solve this problem, Pugh has made a clever transformation: decompose the global, static index building into a separate, dynamic procedure. The key point here is to maintain the query performance by keeping the probability distribution of the global node levels in the SkipList. By analyzing the sampling process above, we can find that 50% of the nodes in SkipList are level 1 nodes, 25% of them are level 2 nodes, 12.5% of them are level 3 nodes, and so on. If we can maintain the same probability distribution for the nodes in our constructed SkipList, we can guarantee that it has the same query performance. This seems intuitively fine, and we will not dive into the mathematics behind it, you could read the paper if you are interested in it.
With such a transformation, the two problems raised above are solved:
The level of new nodes to insert is independently determined each time by calculating a value, such that the node levels globally satisfy the geometric distribution.
No additional node adjustment is required for the insertion. We only need to find the position where it should be placed and then modify its previous and next node pointers.
The time complexity of inserting a node is thus the sum of the time complexity of finding, O(logN), and the complexity of modifying a pointer, O(1), i.e. also O(logN). The deletion process is similar to insertion and can be transformed into binary search and modifying pointers, so the complexity is also O(logN).
LevelDB Source Code
After such a long way, we finally come to the section for the implementation details of SkipList in LevelDB, which is optimized for being accessed concurrently, and provide the following guarantees:
Write: Requires a lock on the user side when modifying the SkipList.
Read: When reading the SkipList (point lookup or range scan), there is no need to add locks, only make sure it should not be destroyed by other threads.
In other words, the user only needs to deal with write-write conflicts and the LevelDB SkipList will handle read-write conflicts.
This is because LevelDB maintains the following invariants:
SkipList nodes could only be added but not deleted unless the SkipList is destroyed entirely, as the SkipList does not expose a delete interface at all.
Fields of inserted nodes are all immutable except for the
nextpointer and only the insertion will change the SkipList.
interface
LevelDB mainly provides 3 interfaces: insertion, point look and range scan.
// Insert key into the list.
// REQUIRES: nothing that compares equal to key is currently in the list.
void Insert(const Key& key);
// Returns true iff an entry that compares equal to key is in the list.
bool Contains(const Key& key) const;
template <typename Key, class Comparator>
inline SkipList<Key, Comparator>::Iterator::Iterator(const SkipList* list);
To support more types, LevelDB's SkipList uses the template class. Then the user could define their customized type and Comparator of Key.
Before going through more details about these interfaces, let's talk about SkipList::Node, the basic elements of SkipList. There are some codes about synchronization and mutually exclusive among many threads for reading and writing shared variables. So let's pause for a while and talk something about instruction reordering here.
We know that the compiler will reorder the code to improve memory usage or accelerate the processing speed. It will be ok for single-thread situations. But for the multi-threads, things become difficult to understand. Let's see an example in golang:
var a, b int
func f() {
a = 1
b = 2
}
func g() {
print(b)
print(a)
}
func main() {
go f()
g()
}
It might surprisingly output 2 0 !
The reason is that the compiler may reorder assignments in the f() or print statements in the g(). We will all think that the codes will be executed exactly as we put them. But the compiler could only guarantee the execution order in the same thread instead of codes in different threads. If you want some codes between threads to execute as you expected, you must use some explicit ways, such as mutex and channel, to restrict it.
Lookup
Lookup is the basis of insertion. That is, we must find the right places before we insert a node. Then LevelDB abstracts a base function, which calls FindGreaterOrEqual.
template <typename Key, class Comparator>
bool SkipList<Key, Comparator>::Contains(const Key& key) const {
Node* x = FindGreaterOrEqual(key, nullptr);
if (x != nullptr && Equal(key, x->key)) {
return true;
} else {
return false;
}
}
FindGreaterOrEqual returns the node if it could find a node not smaller than the given key, else it will return nullptr. If the parameter prev is not null, the function will remember all previous nodes at every level. It is easy to find that this parameter is only useful in the lookup case.
template <typename Key, class Comparator>
typename SkipList<Key, Comparator>::Node*
SkipList<Key, Comparator>::FindGreaterOrEqual(const Key& key, Node** prev) const {
Node* x = head_; // lookup starts from the head_
int level = GetMaxHeight() - 1; // lookup starts from the highest level
while (true) {
Node* next = x->Next(level); // next node in this level
if (KeyIsAfterNode(key, next)) {
x = next; // keep looking in the same level if the given key is bigger
} else {
if (prev != nullptr) prev[level] = x;
if (level == 0) { // return if we reachs the bottom level
return next;
} else { // else just look in the level below
level--;
}
}
}
}
This whole process is illustrated with a figure in the paper:
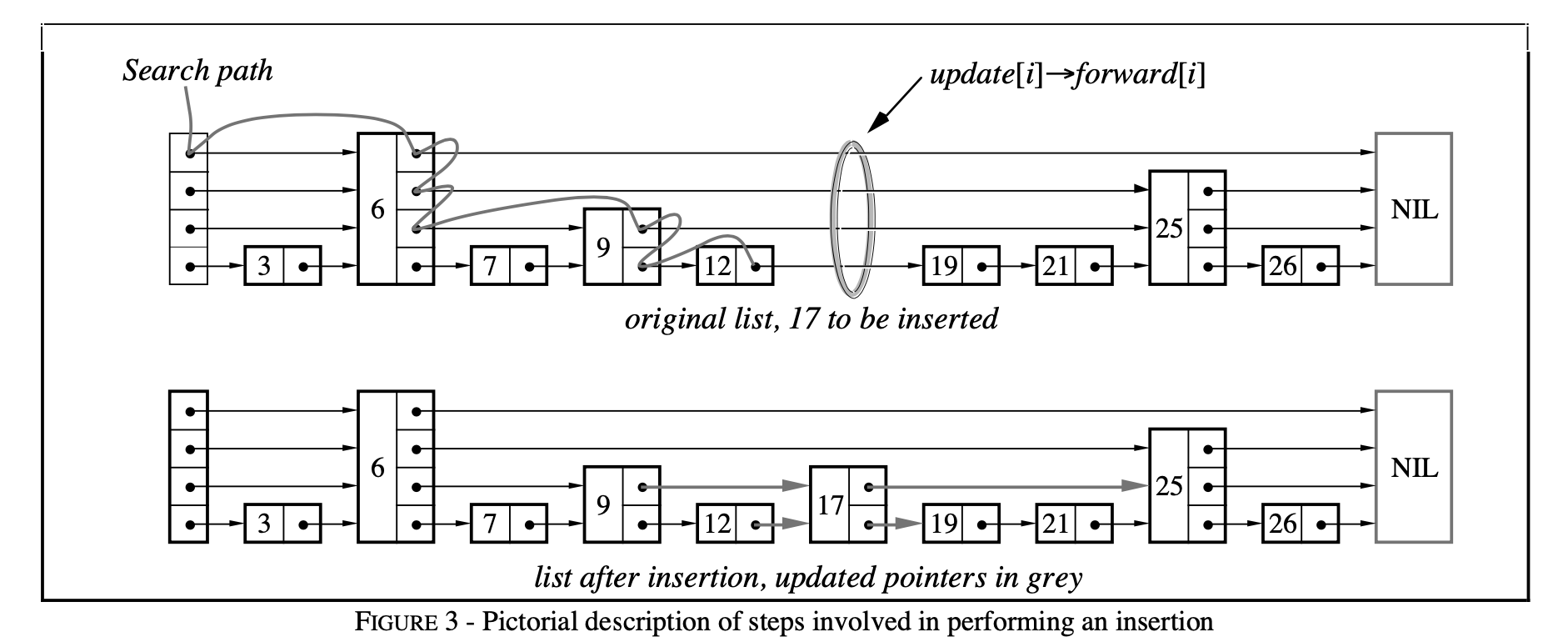
insertion
We first use FindGreaterOrEqual to remember the previous nodes of the given node in each level, then insert it after them. In the figure above, we got prev = [12, 9, 6, 6] for key=17 .
template <typename Key, class Comparator>
void SkipList<Key, Comparator>::Insert(const Key& key) {
Node* prev[kMaxHeight];
Node* x = FindGreaterOrEqual(key, prev);
// LevelDB does not allow inserting same key twice.
assert(x == nullptr || !Equal(key, x->key));
// Get a random height for the node to be inserted.
// If the height
int height = RandomHeight();
if (height > GetMaxHeight()) {
for (int i = GetMaxHeight(); i < height; i++) {
prev[i] = head_;
}
max_height_.store(height, std::memory_order_relaxed);
}
x = NewNode(key, height);
for (int i = 0; i < height; i++) {
x->NoBarrier_SetNext(i, prev[i]->NoBarrier_Next(i));
prev[i]->SetNext(i, x);
}
}.